信息论基础

熵、相对熵与互信息

熵

对于字母表为$\mathcal{X}$的离散随机变量$X$，其概率分布为$p(x),x\in\mathcal{X}$，则熵为

$$H(X)=-\sum_{x\in\mathcal{X}}p(x)\log p(x)=E_p\log\frac{1}{p(X)}$$

熵的性质：

• $H(X)\geq 0$

• 当概率分布为均匀分布时，熵达到最大值，为$\log|\mathcal{X}|$

  证明：令$X\sim p(x)$，$u(x)=\frac{1}{\mathcal{|X|}},x\in\mathcal{X}$

  $$\begin{aligned} D(p||u)&=\sum_{x\in{\mathcal{X}}}p(x)\log\frac{p(x)}{u(x)}\\ &=\log|\mathcal{X}|-H(X)\geq 0\\ \Rightarrow &H(X)\leq \log|\mathcal{X}| \end{aligned}$$

联合熵、条件熵

定义一对离散随机变量$(X,Y)\sim p(x,y)$，其联合熵为

$$H(X,Y)=-\sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}p(x,y)\log p(x,y)$$

条件熵为

$$H(Y|X)=\sum_{x\in\mathcal{X}}p(x)H(Y|X=x)=-\sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}p(x,y)\log p(y|x)$$

链式法则：

$$H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)$$

性质：

• 当$f(X)$为随机离散变量$X$的函数时，$H(f(X)|X)=0$。即已知$X$可以直接推出$f(X)$，该过程没有信息量的增加。

相对熵、互信息

假设概率分布$p(x)$与$q(x)$有相同的字母表$\mathcal{X}$，并满足当$q(x)=0$时，$p(x)=0$，$x\in\mathcal{X}$，则定义相对熵(亦称KL散度)：

$$D(p||q)=\sum_{x\in\mathcal{X}}p(x)\log\frac{p(x)}{q(x)}=E_p\log\frac{p(X)}{q(X)}$$

注意一般$D(p||q)\neq D(q||p)$。

假定$X,Y\sim p(x,y)$，定义在给定另一随机变量知识的条件下，原随机变量不确定度的缩减量为互信息：

$$I(X;Y)=D(p(xy)||p(x)p(y))=\sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}\log\frac{p(x,y)}{p(x)p(y)}$$

性质：

• $I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y)$

  $$\begin{aligned} I(X;Y)&=\sum_{x,y}p(x,y)\log\frac{p(x,y)}{p(x)p(y)}\\ &=\sum_{x,y}p(x,y)\log p(x|y)-\sum_{x,y}p(x,y)\log p(x)\\ &=H(X)-H(X|Y) \end{aligned}$$

• $I(X;Y|Z)=H(X|Z)-H(X|Y,Z)$

• 当$X,Y$相互独立时，$I(X;Y)=0$

• 互信息的链式法则：

  $$I(X_1,X_2,\dots,X_n;Y)=\sum_{i=1}^nI(X_i;Y|X_1,X_2,\dots,X_{i-1})$$

Jensen不等式

在区间$(a,b)$内下凸(convex)的函数$f(x)$，对于任意$x_1,x_2\in(a,b),x_1\neq x_2, 0\leq \lambda \leq 1$，有

$$f(\lambda x_1+(1-\lambda)x_2)\leq\lambda f(x_1)+(1-\lambda)f(x_2)$$

进一步推广，如果$f$为下凸函数，$X$为随机变量，则

$$Ef(X)\geq f(E(X))$$

相对熵的凸性

$D(p||q)$相对于$(p,q)$为凸函数，即对于$\lambda_1+\lambda_2=1,\lambda_1,\lambda_2\geq0$，有

$$D(\lambda_1 p_1+\lambda_2 p_2||\lambda_1q_1+\lambda_2 q_2)\leq \lambda_1 D(p_1||q_1)+\lambda_2 D(p_2||q_2)$$

熵的凹性

$H(p)$为$p$的凹函数：

$$H(p)=\log|\mathcal{X}|-D(p||u)$$

此处$u$为$\mathcal{X}$上的均匀分布。

互信息的凸性

假设$(X,Y)\sim p(x,y)$，对于固定的$p(y|x)$，$I(X;Y)$是$p(x)$的凹函数；对于固定的$p(x)$，$I(X;Y)$是$p(y|x)$的凸函数。

数据处理不等式

如果$p(x,y,z)=p(x)p(y|x)p(z|y)$，则随机变量$X,Y,Z$构成马尔科夫链，记为$X\rightarrow Y\rightarrow Z$，由于马尔科夫链具有对称性，所以$Z\rightarrow Y\rightarrow X$，可以统一记作$X-Y-Z$。

性质：

• 对于任意函数$f$，有$X-Y- f(Y)$

数据处理不等式：如果$X- Y- Z$，则$I(X;Y)\geq I(X;Z)$，即距离越远的随机变量分布差别越大。

证明：

$$I(X;Y,Z)=I(X;Z)+I(X;Y|Z)\\ I(X;Y,Z)=I(X;Y)+I(X;Z|Y)$$

由于$X$与$Z$在条件$Y$下是独立的，则$I(X;Z|Y)=0$，同时$I(X;Y|Z)\geq0$，所以结论得证。

推论：

• 对于任意的函数$f$，$I(X;Y)\geq I(X;f(Y))$

• 如果存在马尔科夫链$X_1-X_2-X_3-X_4$，则$I(X_2;X_3)\geq I(X_1;X_4)$

• 如果存在马尔科夫链$X-Y-Z$，则$I(X;Y)\geq I(X;Y|Z)$，可由数据处理不等式的证明得到。

Fano不等式

对于任意似然估计量$\hat{X}$，满足马尔科夫链$X-Y-\hat{X}$，定义$P_e=\text{Pr}(X\neq \hat{X})$，有

$$H(P_e)+P_e\log|\mathcal{X}|\geq H(X|\hat{X})\geq H(X|Y)$$

这里$\hat{X}$的字母表不一定要和$X$一样。

推论：对于随机变量$X,Y$，$p=\text{Pr}(X\neq Y)$，则有$H(p)+p\log|\mathcal{X}|\geq H(X|Y)$

Fano不等式可进一步放缩为$1+p\log|\mathcal{X}|\geq H(X|Y)$

证明：定义随机变量

$$E=\left\{\begin{aligned} &1 \text{ if } \hat{X}\neq X\\ &0 \text{ otherwise} \end{aligned}\right.$$

考虑

$$H(E,X|\hat{X})=H(X|\hat{X})+H(E|X,\hat{X})=H(E|\hat{X})+H(X|E,\hat{X})$$

一方面

$$H(E|\hat{X})\leq H(E)=H(P_e)$$

另一方面

$$\begin{aligned} H(X|E,\hat{X})&=\text{Pr}(E=0)H(X|\hat{X},E=0)+\text{Pr}(E=1)H(X|\hat{X},E=1)\\ &\leq (1-P_e)\cdot 0+ P_eH(X)\\ &\leq P_e\log|\mathcal{X}| \end{aligned}$$

所以

$$H(P_e)+P_e\log|\mathcal{X}|\geq H(X|\hat{X})$$

渐进均分性质(AEP)

随机变量$X\sim p(x),x\in\mathcal{X}$产生的独立同分布随机序列$X^n=(X_1,X_2,\dots,X_n)$。所有可能的采样有$|\mathcal{X}|^n$个，而典型集的大小为$|A_{\epsilon}^{(n)}|\approx2^{nH(X)}$

弱大数定律

考虑独立同分布的随机变量$X_1,X_2,\dots,X_n$，分布的均值为$EX$，定义

$$\overline{X}_n=\frac{1}{n}\sum_{i=1}^nX_i$$

则有

$$\lim\limits_{n\rightarrow \infty}\text{Pr}(|\overline{X}_n-EX|>\epsilon)=0$$

强大数定律

$$\text{Pr}\left(\lim\limits_{n\rightarrow \infty}\overline{X}_n=EX\right)=1$$

概率论中的收敛

• $X_n\overset{D}{\rightarrow}X$依分布收敛：如果函数$F_X(x)=\text{Pr}(X\leq x)$是连续的，当$x\rightarrow \infty$时$\text{Pr}(X_n\leq x)\rightarrow \text{Pr}(X\leq x)$
• $X_n\overset{P}{\rightarrow}X$依概率收敛：对于任意$\epsilon>0$，$\text{Pr}\{|X_n-X|>\epsilon\}\rightarrow 0$
• $X_n\overset{a.s.}{\rightarrow}X$以概率1收敛：$\text{Pr}\left\{\lim\limits_{n\rightarrow \infty}X_n=X\right\}=1$
• $X_n\overset{r}{\rightarrow}X$依$L^r$范数收敛

AEP

随机变量$X\sim p(x),x\in\mathcal{X}$产生的独立同分布随机序列$X^n=(X_1,X_2,\dots,X_n)$，有

$$-\frac{1}{n}\log p(X_1,X_2,\dots,X_n)\overset{P}{\rightarrow}H(X)$$

AEP表明观测到的序列的概率$p(x_1,x_2,\dots,x_n)$将会收敛于$2^{-nH(X)}$。

典型集的定义：如果所有长度为$n$的序列$(x_1,\dots,x_n)$所构成的集合满足

$$2^{-n(H(X)+\epsilon)}\leq p(x_1,x_2,\dots,x_n)\leq2^{-n(H(X)-\epsilon)}$$

等价于

$$|-\frac{1}{n}\log p(x_1,\dots,x_n)-H(X)|\leq \epsilon$$

则称该集合为典型集。

典型集的性质：

• $\forall (x_1,\dots,x_n)\in A_{\epsilon}^{(n)}$，$H(X)-\epsilon \leq -\frac{1}{n}\log p(x_1,x_2,\dots,x_n)\leq H(X)+\epsilon$

• 当$n$足够大时，$\text{Pr}\{A_{\epsilon}^{(n)}\}>1-\epsilon$

• 当$n$足够大时，$(1-\epsilon)2^{n(H(X)-\epsilon)}\leq |A_{\epsilon}^{(n)}| \leq 2^{n(H(X)+\epsilon)}$

AEP与数据压缩的关系

$X_1,X_2,\dots,X_n$是从分布$p(x)$采样出的独立同分布随机变量，数据压缩的目的是寻找用于描述这些随机变量的更短的序列。将$\mathcal{X}^n$中的所有序列分为典型集$A_{\epsilon}^{(n)}$与非典型集$(A_{\epsilon}^{(n)})^c$，则可以使用$nH(X)$个比特以任意小的误差概率来表征序列$\mathcal{X}^n$。即压缩前需要的比特数：$n\log_2|\mathcal{X}|$，压缩后的比特数：$nH(X)$。

数据压缩

定义

信源编码$C$对应一个随机变量$X$，

由$\mathcal{X}$到$D^*$（由字母表$D$中的符号组成的有限长字符）的映射。用$C(x)$表示$x\in\mathcal{X}$对应的codeword，$l(x)$表示$C(x)$的长度，即$C(x)\in D^{l(x)}$。

对于概率分布为$p(x)$的随机变量$X$，$C(x)$的期望长度$L(C)$为

$$L(C)=\sum_{x\in\mathcal{X}}p(x)l(x)$$

定义

$$C(x_1x_2\dots x_n)=C(x_1)C(x_2)\dots C(x_n)$$

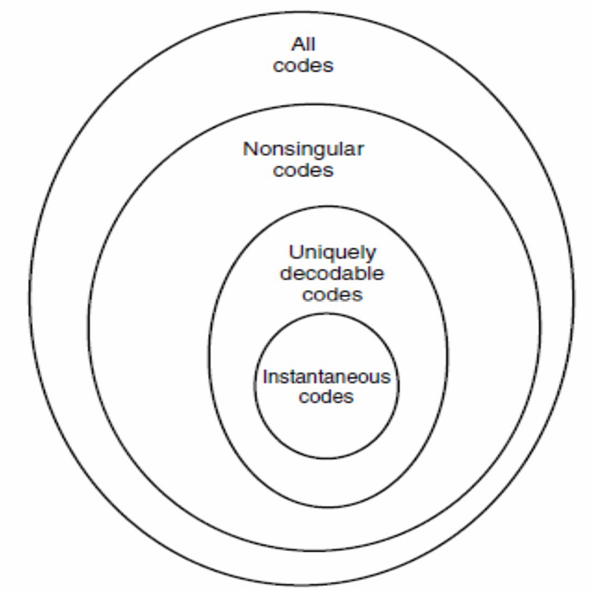
根据编码不同的特点给出定义：

• 如果编码能实现一一映射，则称其为非奇异的。

• 如果一个编码的扩展编码是非奇异的，则称其为唯一可译的。

• 如果没有编码是其他编码的前缀则称为前缀码或即时码。

举例：对于字母表$\mathcal{X}=\{1,2,3,4\}$

非奇异码：$C(1)=0,C(2)=1,C(3)=10,C(4)=11$

唯一可译码：$C(1)=10,C(2)=00,C(3)=11,C(4)=110$

即时码：$C(1)=0,C(2)=10,C(3)=110,C(4)=111$

不同码的包含关系：

Kraft不等式

对于任意大小为$D$的字母表下的前缀码，码长$l_1,l_2,\dots,l_m$必定满足不等式

$$\sum_{i}D^{-l_i}\leq1$$

从另一个角度，如果给定一系列满足上述不等式的长度，则存在对应这些长度的前缀码。

最优码

任意前缀码长的下界：对于字母表大小为$D$的随机变量$X$，其前缀码的期望码长$L$满足：

$$L\geq H_D(X)$$

当且仅当$D^{-l_i}=p_i$时等号成立。$H_D(X)$表示以$D$为对数底数时的熵。

Shannon码

$$l_i=\lceil\log_D\frac{1}{p_i}\rceil$$

可以看出其满足Kraft不等式：

$$\sum D^{-\lceil log_D\frac{1}{p_i}\rceil}\leq \sum D^{-\log_D\frac{1}{p_i}}=\sum p_i=1$$

所以满足上述码长$\{l_i\}$总是存在的，码长的选择满足

$$\log_D\frac{1}{p_i}\leq l_i < \log_D\frac{1}{p_i}+1$$

求概率加权和可以得到

$$H_D(X)\leq L <H_D(X)+1$$

从而可以得到最优码的上下界：

$$H_D(X)\leq L^*\leq H_D(X)+1$$

Huffman码

Huffman是最优码，即如果$C^*$是Huffman码而$C$是其他唯一可译码，则有

$$L(C^*)\leq L(C)$$

引理：对于任意分布，总存在最优即时码满足以下属性：

• 码长满足：如果$p_i>p_j$，则$l_j\leq l_k$

• 最长的两个码字长度相同。

• 最长的两个码字只在最后一个比特上不同，并对应着两个最低概率的符号。

信道容量

离散信道

定义：包含输入字母表$\mathcal{X}$输出字母表$\mathcal{Y}$与概率转移矩阵$p(y|x)$的系统。

如果输出的概率分布只依赖于相同时间的输入，与先前的输入、输出无关，则该信道是无记忆的，即

$$Y_i-X_i-((X_1,\dots,X_{i-1},X_{i+1},\dots,X_n),(Y_1,\dots,Y_{i-1},Y_{i+1},\dots,Y_n))\\ p(y^n|x^n)=\prod_{i=1}^{n}p(y_i|x_i)$$

信道容量：能以极低错误概率进行传输时的传输速率。离散无记忆信道的信道容量为

$$C=\underset{p(x)}{\max}I(X;Y)$$

取最大值需要遍历所有可能的输入分布$p(x)$。

信道容量的性质：

• $C\geq 0$

• $C\leq\log|\mathcal{X}|,C\leq\log\mathcal{Y}$

• $I(X;Y)$是$p(x)$的连续上凸函数

特殊信道的信道容量

• 二元对称信道：

  $$\begin{aligned} I(X;Y)&=H(Y)-H(Y|X)\\ &=H(Y)-\sum p(x)H(Y|X=x)\\ &=H(Y)-\sum p(x)H(p)\\ &=H(Y)-H(p)\\ &\leq 1-H(p) \end{aligned}$$

  所以$C\leq 1_H(p)$，令$p(x=0)=p(x=1)=\frac{1}{2}$，有$H(Y)=1$，所以$C=1-H(p)$。

• 二元擦除信道：传输中一些比特丢失或被混淆且接收端能分辨出哪些比特被擦除。

  假设$p(x=1)=1-p(x=0)=\pi$。出现擦除记为$Y=e$，$p(Y=e)=\alpha$，则

  $$\begin{aligned} I(X;Y)&=H(Y)-H(Y|X)\\ &=H(Y)-H(\alpha)\\ &=H(Y,E)-H(\alpha)\\ &=H(E)+H(Y|E)-H(\alpha)\\ &=H(\alpha)+(1-\alpha)H(\pi)-H(\alpha)\\ &=(1-\alpha)H(\pi) \end{aligned}$$

  其中$H(Y|E)=p(Y=e)H(Y|Y=e)+p(Y\neq e)H(Y|Y\neq e)=(1-\alpha)H(\pi)$

  所以$C=\underset{\pi}{\max}(1-\alpha)H(\pi)=1-\alpha$，当$\pi=\frac{1}{2}$，可以达到信道容量。

• 对称信道：对于转移矩阵，如果每行$p(\cdot|x)$是其他行的另一种排列且每一列的和$\sum_x p(y|x)$都相同，则该信道称为弱对称信道。如果每行、每列都是各自的排列则该信道称为对称信道。

  如

  $$p(y|x)=\left(\begin{matrix} \frac{1}{3}&\frac{1}{6}&\frac{1}{2}\\ \frac{1}{3}&\frac{1}{2}&\frac{1}{6} \end{matrix}\right)$$

  为弱对称信道，

  $$p(y|x)=\left(\begin{matrix} 0.3&0.2&0.5\\ 0.5&0.3&0.2\\ 0.2&0.5&0.3 \end{matrix}\right)$$

  为对称信道。

定理：任意弱对称信道的容量为

$$C=\log|\mathcal{Y}|-H(\vec{r})$$

此处$\vec{r}$为转移矩阵中的任意一行，同时输入分布为均匀分布时可以达到信道容量。

联合典型序列

设$(X^n,Y^n)$为服从$p(x^n,y^n)=\prod _{i=1}^n p(x_i,y_i)$的独立同分布的$n$长序列，则

• 当$n\rightarrow \infty$时，$\text{Pr}((X^n,Y^n)\in A_{\epsilon}^{(n)})\rightarrow 1$

• $|A^{(n)}_{\epsilon}|\leq2^{n(H(X,Y)+\epsilon)}$

• 如果$(\tilde{X}^n.\tilde{Y}^n)\sim p(x^n)p(y^n)$，即$\tilde{X}^n$与$\tilde{Y}^n$是独立的且与$p(x^n,y^n)$有着相同的边际分布，那么

  $$\text{Pr}((\tilde{X}^n,\tilde{Y}^n)\in A_{\epsilon}^{(n)})\leq2^{-n(I(X;Y)-3\epsilon)}$$

  而且对于充分大的$n$，

  $$\text{Pr}((\tilde{X}^n,\tilde{Y}^n)\in A_{\epsilon}^{(n)})\geq(1-\epsilon)2^{-n(I(X;Y)+3\epsilon)}$$

信道编码定理

对于离散无记忆信道，如果$R<C$，则存在一系列$(2^{nR},n)$编码可以使得误差概率趋近于0。

Source-channel coding theorem

如果$V_1,V_2,\dots,V_n$为有限字母表上满足AEP和$H(\mathcal{V})C$，那么误差概率远离0，从而不可能以任意低的误差概率通过信道发送这个过程。

乘积信道与选择性信道

乘积信道：$C=C_1+C_2$

选择性信道：$2^C=2^{C_1}+2^{C_2}$

微分熵

微分熵的定义

令概率分布$f(x)>0$的所有$x$构成的集合称为支撑集。

对于概率分布为$f(x)$连续随机变量$X$的微分熵定义为

$$h(X)=-\int_Sf(x)\log f(x)dx$$

例如正态分布$X\sim\mathcal{N}(0,\sigma^2)$的微分熵为

$$h(x)=\frac{1}{2}\ln2\pi e\sigma^2 \text{ nats}$$

微分熵可以为零以及负数。

证明：设$X\sim \phi(x)=\frac{1}{\sqrt{2\pi \sigma^2}}\exp(\frac{-x^2}{2\sigma^2})$

$$\begin{aligned} h(\phi)&=-\int \phi\ln\phi dx\\ &=-\int \phi(x)(-\frac{x^2}{2\sigma^2}-\ln\sqrt{2\pi\sigma^2})dx\\ &=\frac{E(X^2)}{2\sigma^2}+\frac{1}{2}\ln 2\pi \sigma^2\\ &=\frac{1}{2}\ln 2\pi e\sigma^2\text{ nats}\\ &=\frac{1}{2}\log 2\pi e \sigma^2 \text{ bits} \end{aligned}$$

联合微分熵与条件微分熵

假设$(X,Y)\sim f(x,y)$，则

$$h(X,Y)=-\int\int f(x,y)\log f(x,y)dxdy\\ h(X|Y)=-\int\int f(x,y)\log f(x|y)dxdy$$

所以有$h(X|Y)=h(X,Y)-h(Y)$

定理：假设$(X_1,X_2,\dots,X_n)\sim\mathcal{N}(\vec \mu,K)$，$K$为协方差矩阵，则

$$h(X_1,X_2,\dots,X_n)=\frac{1}{2}\log(2\pi e)^n|K| \text{ bits}$$

相对熵与互信息

两个连续随机变量概率分布$f$与$g$之间的KL散度定义为：

$$D(f||g)=\int f\log\frac{f}{g}$$

联合概率分布为$f(x,y)$，则互信息为

$$I(X;Y)=D(f(x,y)||f(x)f(y))=\int f(x,y)\log\frac{f(x.y)}{f(x)f(y)}dxdy$$

由定义可得

$$I(X;Y)=h(X)-h(X|Y)=h(Y)-h(Y|X)=h(X)+h(Y)-h(XY)$$

微分熵的性质

• 平移变换不会改变微分熵：$h(X)=h(X+C)$

• $$h(AX)=h(X)+\log|\text{det}(A)|$$

  这里$A$为非奇异方阵，当$A$变为单个标量时，有$h(aX)=h(X)+\log|a|$

定理：令随机变量$X\in \mathbb{R}^n$的均值为0，协方差矩阵为$K$，则

$$h(X)\leq \frac{1}{2}\log(2\pi e)^n|K|$$

当且仅当$X\sim\mathcal{N}(0,K)$时等号成立。

推论：给定随机变量$X\in\mathbb{R}^n$与$Y$，有

$$h(X|Y)\leq \frac{1}{2}\log(2\pi e)^n|D_{X|Y}|$$

高斯信道

高斯信道的定义

$Y=X+Z,Z\sim\mathcal{N}(0,N)$，同时$Z$可以认为与$X$独立。可以使用$(\mathbb{R},f(y|x),\mathbb{R}),f(y|x)=\frac{1}{\sqrt{2\pi N}}\exp\left[-\frac{(y-x)^2}{2N}\right]$来表示该信道。

高斯信道的限制之一为输入能量受限，即对于任意码字$(x_1,x_2,\dots,x_n)$满足

$$\frac{1}{n}\sum_{i=1}^n x_i^2\leq P$$

高斯信道的信道容量

$$\begin{aligned} I(X;Y)&=h(Y)-h(Y|X)\\ &=h(Y)-h(X+Z|X)\\ &=h(Y)-h(Z|X)\\ &=h(Y)-\frac{1}{2}\log 2\pi e N \end{aligned}$$

由于$EY^2=E(X+Z)^2=EX^2+EZ^2=P+N$，所以$h(Y)\leq\frac{1}{2}\log2\pi e(P+N)$，所以信道容量$C=\frac{1}{2}\log(1+\frac{P}{N})$，可在$X\sim \mathcal{N}(0,P)$时达到。

注水算法

$$\sum_{i=1}^n(\frac{1}{2\lambda}-N_i)^+=P$$

率失真理论

失真度量

失真函数定义为：

$$d:\mathcal{X}\times \mathcal{X}\rightarrow \mathbb{R}^+$$

一些失真函数：

• Hamming失真：

  $$d(x,\hat{x})=\left\{\begin{aligned} 0,x=\hat{x}\\ 1,x\neq \hat{x} \end{aligned}\right.$$

• 平方误差失真：

  $$d(x,\hat{x})=(x-\hat{x})^2$$

序列的失真度量：

$$d(x^n,\hat{x}^n)=\frac{1}{n}\sum_{i=1}^n d(x_i.\hat{x}_i)$$

对于包含编码函数$f_n$与译码函数$g_n$的一个$(2^{nR},n)$的率失真码的失真定义为

$$D=\sum_{x^n}p(x^n)d(x^n,g_n(f_n(x^n)))$$

该失真为针对$X$的分布的期望值。

率失真函数

对于给定的失真$D$，满足$(R,D)$包含于信源的率失真区域中所有码率$R$的下确界称为率失真函数$R(D)$。

对于给定的码率$R$，满足$(R,D)$包含于信源的率失真区域中所有失真$D$的下确界称为失真率函数$D(R)$。

设信源$X$的失真度量为$d(x,\hat{x})$，定义其信息率失真函数$R^{(I)}(D)$为：

$$R^{(I)}(D)=\underset{p(\hat{\mathcal{X}|}\mathcal{X}):Ed(X,\hat{X})\leq D}{\min}I(X;\hat{X})$$

此处$Ed(X,\hat{X})=\sum_{\mathcal{X},\hat{\mathcal{X}}}p(x)p(\hat{x}|x)d(x,\hat{x})$。最小值由遍历所有条件概率分布得到。

特殊信源的率失真函数

满足分布$\text{Bernoulli}(p)$二元信源的Hamming率失真函数：

$$R(D)=\left\{ \begin{aligned} &H(p)-H(D),&0\leq D\leq \text{min}(p,1-p)\\ &0,&D>\text{min}(p,1-p) \end{aligned} \right.$$

证明：

$$\begin{aligned} I(X;\hat{X})&=H(X)-H(X|\hat{X})\\ &=H(p)-H(X\oplus \hat{X}|\hat{X})\\ &\geq H(p)-H(X\oplus \hat{X})\\ &\geq H(p)-H(D) \end{aligned}$$

高斯信源$\mathcal{N}(0,\sigma^2)$的平方误差率失真函数：

$$R^{(I)}{(D)}=\left\{ \begin{aligned} &\frac{1}{2}\log\frac{\sigma^2}{D},&0\leq D\leq\sigma^2\\ &0,&D>\sigma^2 \end{aligned} \right.$$

证明：

$$\begin{aligned} I(X;\hat{X})&=h(X)-h(X|\hat{X})\\ &=\frac{1}{2}\log 2\pi e\sigma^2-h(X-\hat{X}|\hat{X})\\ &\geq \frac{1}{2}\log 2\pi e\sigma^2-h(X-\hat{X})\\ &\geq \frac{1}{2}\log 2\pi e\sigma^2-h(\mathcal{N}(0,E(X-\hat{X})^2))\\ &=\frac{1}{2}\log 2\pi e\sigma^2-\frac{1}{2}\log 2\pi eE(X-\hat{X})^2\\ &\geq \frac{1}{2}\log 2\pi e\sigma^2-\frac{1}{2}\log 2\pi eD\\ &=\frac{1}{2}\log\frac{\sigma^2}{D} \end{aligned}$$

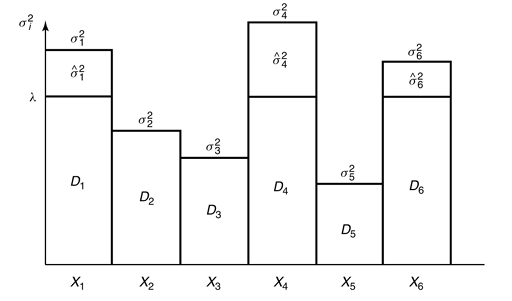
反注水算法

有$m$个正态随机信源$X_i\sim\mathcal{N}(0,\sigma_i^2)$相互独立，失真由$d(x^m,\hat{x}^m)=\sum_{i=1}^m(x_i-\hat{x}_i)^2$衡量，给定$D<\sum_{i=1}^m\sigma_i^2$（即总失真为固定值），需要如何分配失真使得总码率需求最低？

每个信源的率失真函数为

$$R(D)=\sum_{i=1}^m\frac{1}{2}\log\frac{\sigma_i^2}{D_i}$$

此处

$$D_i=\left\{\begin{aligned} \lambda,\text{if }\lambda \leq \sigma_i^2\\ \sigma_i^2,\text{if }\lambda\geq\sigma_i^2 \end{aligned}\right.$$

$\lambda$的取值满足$\sum_{i=1}^mD_i=D$，也即$D_i=\min(\lambda,\sigma_i^2)$