ANS算法

Asymmetric numeral systems: entropy coding combining speed of Human coding with compression rate of arithmetic coding

参考博客：Lossless Compression with Asymmetric Numeral Systems | Bounded Rationality

背景知识

对于数据编码定义以下概念：

• bits：即数字通信中的0、1。
• symbol：信息传输的单位，可以为bits或者由一系列bits表示的更高层次的概念，如”a”、”b”等。
• alphabet：包含传输所有符号的集合。
• message：由一系列symbols组成。

数据压缩存在理论上限值，根据香农的信源信源编码定理，数据无损压缩的理论上限即数据本身的熵，即编码每个符号的平均比特数不可能小于：

$$H(X)=-\sum_{i=1}^n p_i\log_2 p_i$$

考虑符号${a,b,c}$的两种分布情况$(\frac{4}{7},\frac{2}{7},\frac{1}{7})$与$(\frac{1}{3},\frac{1}{3},\frac{1}{3})$，前者的熵为$H(X)=1.3788\text{bits}$，后者为$H(X)=1.5850\text{bits}$。这说明平均分布的符号是最难压缩的，因为无法找到符号分布中的不对称性。

Asymmetric numeral systems的介绍

可以假设字节流$b_1b_2b_3\dots b_i$通过二进制转十进制编码为自然数$x_i$，则获得字节$b_{i+1}$时，可以使用以下方式进行编码：

$$C(x_i,b_{i+1}):=2x_i+b_{i+1}$$

同样，基于自然数$x_i$，也可以通过迭代的方式逐步输出$b_i$与$x_{i-1}$：

$$(x_{i-1}, b_i)=D(x_{i}):=(\lfloor \frac{x_i}{2}\rfloor), x_{i} \text{mod}{2})$$

有以下注意点：

• 为了区分”0”、”00”等，应该初始化$x_0=1$。
• 上述情况在0、1均匀分布时达到最优，即与二进制转十进制的方式相对应。

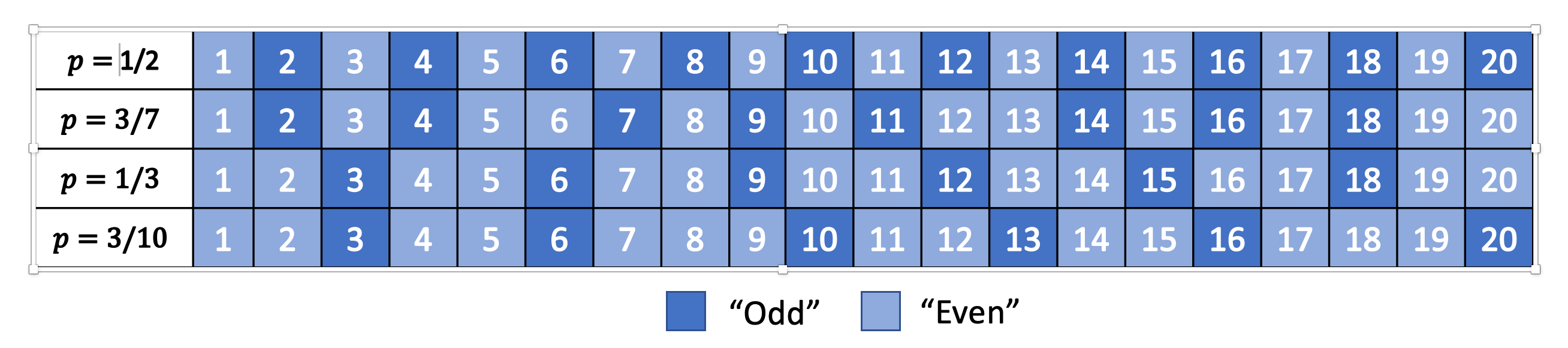
对于字节流也给出奇偶的定义，即以0结尾的字节流视为偶数，以0结尾的字节流视为奇数。

在上述编码中，$p_0=p_1=\frac{1}{2}$，字节流的奇数与偶数与自然数$x_i$的奇数与偶数一一对应。对于0、1分布不均匀的情况，假定$p_1=p<1-p=p_0$，即对于任意一串字节流，以0结尾的概率大于以1结尾的概率，则应期望在给定范围内偶数字节流映射到的自然数的个数大约为奇数字节流映射自然数个数的$\frac{1-p}{p}$。或者说，给定在$[1,N]$范围内的自然数，其中代表奇数字节流与偶数字节流的自然数分别有$N\cdot p$与$N\cdot (1-p)$个。

此时需要寻找一个最优的编码方式。从信息论的角度分析，自然数$x_i$包含的信息量为$\log_2x_i$，对于出现概率为$p_{b_{i+1}}$的$b_{i+1}$其信息量为$\log_2 \frac{1}{p_{b_{i+1}}}$，则添加该符号后整体的信息量$\log_2 x_{i+1}=\log_2 {x_i}+\log_2 \frac{1}{p_{b_{i+1}}}=\log_2 \frac{x_i}{p_{b_{i+1}}}$，那么最优的编码方式即为$C_{opt}(x_i,b_{i+1}) \approx \frac{x_i}{p_{b_{i+1}}}$

通过上面的分析，对于不均匀分布的0、1找到了最优的编码方式。这也是ABS的思路。

Uniform Binary Variant(uABS)

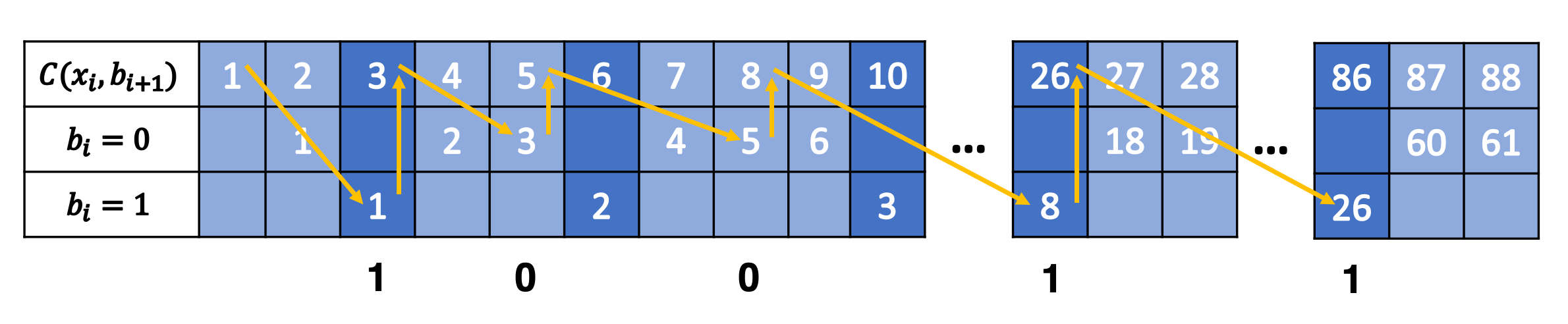
继续上面的分析，当0、1满足$p_1=p<1-p=p_0$时，则前$N$个自然数大约有$N \cdot p$个被映射到1所对应的字符串。为了保证结果为整数，向上取整，则有

$$\lceil(N+1)\cdot p\rceil-\lceil N\cdot p\rceil=\left\lbrace \begin{aligned} &1,\text{if } b_{b+1}=0\newline &0,\text{otherwise} \end{aligned}\right.$$

可以证明下面的编码函数满足上式所具有的特性：

$$C(x_i,b_{i+1})=\left\lbrace \begin{aligned} &\lceil\frac{x_i+1}{1-p} \rceil-1 \quad &\text{if} \space b_{i+1}=0\newline &\lfloor \frac{x_i}{p} \rfloor, &\text{otherwise} \end{aligned} \right.$$

对应的解码函数$(x_i,b_{i+1})=D(x_{i+1})$满足：

$$b_{i+1}=\lceil(x_{i+1}+1) \cdot p\rceil-\lceil x_{i+1}\cdot p\rceil\\ x_i=\left\lbrace \begin{aligned} &x_{i+1}-\lceil x_{i+1}\cdot p\rceil, &\text{if }b_{i+1}=0\newline &\lceil x_{i+1}\cdot p\rceil,& \text{otherwise} \end{aligned} \right.$$

uABS的编码过程可以使用映射表可视化：

Range Variants(rANS)

uABS还是基于包含0、1的alphabet，实际上可以进一步分析任意尺寸的alphabet。ABS中的编码函数对于符号也是通用的：$C_{opt}(x_i,s_{i+1}) \approx \frac{x_i}{p_{s_{i+1}}}$，即增加一个symbol应只增加$\log_2\frac{x_i}{p_{s_{i+1}}}$比特的信息熵。为了避免大型alphabet对于寻找合适编解码函数的麻烦，将分布量化为$2^n$个块，则$p_s\approx \frac{f_s}{2^n}$，此处$f_s$为自然数。

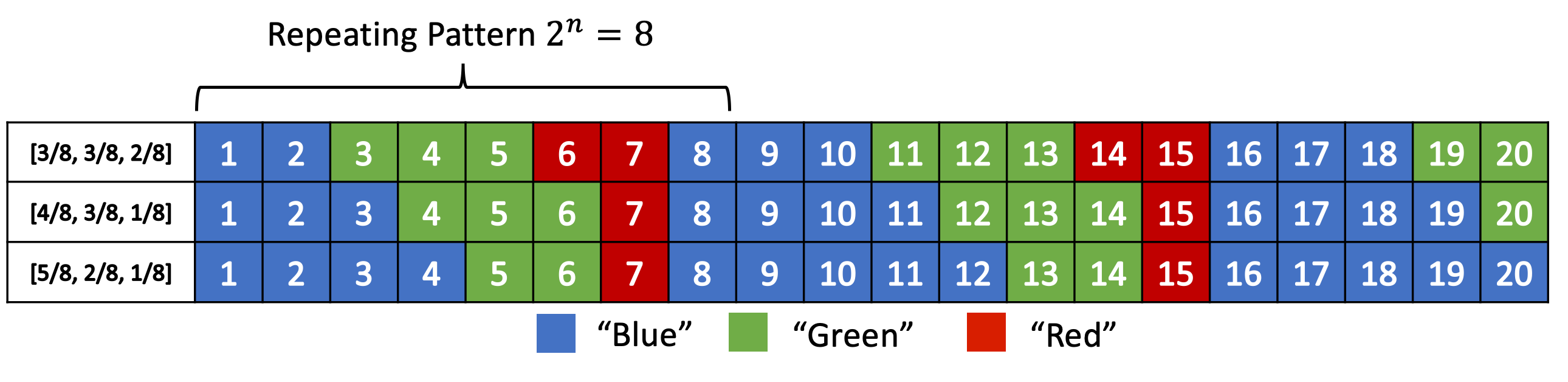
此时采用以下编解码方式：

$$\begin{aligned} &C(x_i, s_{i+1}):=\lfloor \frac{x_i}{f_s}\rfloor\cdot 2^n+\text{CDF}[s]+(x_i\text{ mod }f_s)\newline& s_{i+1}=\text{symbol}(x_{i+1}\text{ mod }2^n) \text{ such that CDF}[s]\leq x_{i+1}\text{ mod }2^n < \text{CDF}[s+1]\newline& x_i=f_s\cdot \lfloor \frac{x_{i+1}}{2^n}\rfloor-\text{CDF}[s]+(x_{i+1}\text{ mod }2^n)& \end{aligned}$$

此处$\text{CDF}[s]:=\sum_{i=1}^{s-1}f_i$。实际上，由于将分布量化为了2的指数幂，乘除可以直接进行移位操作。

Renormalization

对于较长的字节流，实际上不能用自然数直接去表示，这里使用到的技巧是保证$x_i\in[2^M,2^{2M}-1]$，即当$x_i$过大时，仅保留最低的$M$位置来保证其位于$[2^M,2^{2M}-1]$，这里的$M$可以设为16等。在解码过程中，如果$x_i$过小，则将当前数字移位并读取$M$为作为低$M$位。伪代码如下：

MASK = 2**M - 1
BOUND = 2**(2*M) - 1

# Encoding
s = readSymbol()
x_test = (x / f[s]) << n + (x % f[s]) + c[s]
if (x_test > BOUND):
    write16bits(x & MASK)
    x = x >> M
x = (x / f[s]) << n + (x % f[s]) + c[s]

# Decoding
s = symbol[x & MASK]
writeSymbol(s)
x = f[s] (x >> n) + (x & MASK) - c[s]
if (x < 2**M):
    x = x << M + read16bits()