基于熵编码VAE的图像压缩模型
Keyword: lossy image compress, prior model, hyper prior model, context model.
End-to-end Optimized Image Compression
Introduction
提出的观点:图像压缩的目的是对于给定的离散数据设计最小熵的编解码器,极度依赖于对于数据概率分布的先验。一般连续的数据必须要量化为有限的离散值,这引入了误差,这样的压缩即为有损压缩。这种情况下则必须权衡两方面:离散表征的熵(rate)与量化引入的误差(distortion)。
传统压缩方式是使用线性变换将原始数据转换为合适的连续数值表征,再对其单独进行量化,然后使用无损熵编码对这些量化后的离散表征进行压缩。这种压缩方式又称为变换编码(transform coding),如JPEG在每个8*8的像素块熵使用离散余弦变换;JPEG2000使用多尺度正交小波分解。一般这里面的三个部分——变换、量化、熵编码是通过人为定义分别优化的。
端到端的图像压缩模型内,使用级联的线性卷积层和非线性函数作为变换,然后使用均匀量化,之后再使用参数表征的非线性逆变换获得量化后的原始图像。
Overall Architecture
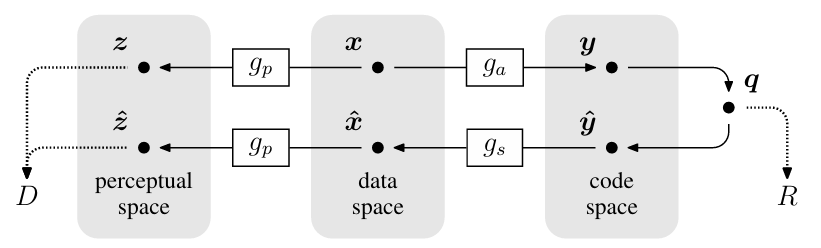
提出了非线性编码的总体框架,可实现码率和失真率直接的平衡控制。框架包含:
- $g_a$、$g_s$:实现图像数据域与编码域之间的变换,$y=g_a(x;\phi),\hat x=g_s(\hat y;\theta)$,对$y$进行量化得到$q$,对$q$进行编码得到对应的码率$R$
- $g_p$:一个固定的变换,实现将图像转换到感知域$\hat z=g_p(\hat x)$,进行原图像与重建图像的对比,得到失真度$D$
对上述模型的优化集中在$\phi$与$\theta$上,可定义损失函数为$R+\lambda D$,通过修改$\lambda$来控制模型的R-D性能。
Choice of Forward, Inverse, and Perceptual Transforms
$g_a$包含卷积、下采样与GDN。以$u_i^{(k)}(m,n)$代表第$k$层第$i$个通道,位置为$(m,n)$的元素。
则输入图像为$u_i^{(0)}(m,n)$,输出为$u_i^{(3)}(m,n)$,每一阶段可表示为先卷积
再下采样
之后进行GDN操作
对于解码方式,则与上述操作相反,分别用反卷积、上采样、IGDN代替。
Optimization of Nonlinear Transform Coding Model
目标函数
这里的期望由数据集所有图片求均值得到。为了编码使用更小的码率,要求编码的熵尽可能小,即降低$-\mathbb E[\log_2 P_q]$,为了保证图片重建质量,则需与原图的差距尽可能小,即降低$\mathbb E[d(z,\hat z)]$
可微分量化
一般的分段量化遵循:
此时$\hat y_i$的离散概率分布可表示为脉冲函数的加权积分:
上述的分段量化会存在边界不可导、其余位置导数为0的问题。论文中使用加性均匀噪声,即在$y$上添加了服从$\mathcal U(-0.5,0.5)$的噪声$\Delta y$:$\tilde{y}=y+\Delta y$来替代对$y$直接进行分段量化$q$,则
此时$\tilde y$的可微分熵可用于近似$q$的熵。
这里$p_{\tilde y_i}=p_{y_i}*\mathcal U(0,1)$相当于对$p_{y_i}$进行平滑,模型的量化误差可以通过减小均匀分布的范围进行任意的缩小。
使用上述加性均匀噪声的量化方法,损失函数可写为
与VAE的关联
在VAE的推理过程中,需要模型找到后验分布$p_{y|x}(y|x)$。可以通过定义分布$q(y|x)$计算KL散度去进行拟合:
定义生成模型(解码器)为
近似的后验分布为
此处$\mathcal U(\tilde y_i;y_i,1)$代表中心位于$y_i$,单位长度的均匀分布。
此时,KL散度第一项为常数,第二项对应失真度,第三项对应码率。
VAE的图像重建任务在对应于$R+\lambda D$中$\lambda\rightarrow \infty$的情况。
Variational Image Compression With a Scale Hyperprior
传统压缩方法可通过传送边信息(side information, 从编码器发送给解码器的多余比特信息,用于调整熵编码模型来减少错配)。以这种方式,要求平均的边信息比特量要少于减少到编码比特量。
比如,JPEG对每个图像均使用$8\times8$的分块方式,对于大面积的低频区域,实际上可以使用更大的分块来有效进行编码,而HEVC则可以预先选择分块的大小,并将其存储在边信息中。
论文中基于该问题,提出了对熵编码模型的隐含表示的学习。论文中尝试证明边信息可以视为熵编码模型的先验条件,即作为hyperprior。
码率对应压缩表征的期望码长,可以使用交叉熵进行表示:
Introduction of a Scale Hyperprior
对于$\hat y$,在空间域上不同元素直接存在相关性,因此引入了额外的随机变量$\hat z$来消除$\hat y$在空间上的相关性。
每个元素$\hat y_i$被建模为零均值高斯分布,方差对应为$\sigma_i$,其值由$\hat z$通过变换$h_s$预测得到:
实现的模型为在原先模型上添加从$y$至$z$的变换$h_a$,从而构建可分解的联合后验分布:
对$\tilde z$进行建模:
Univariate Non-Parametric Density Model
Ballé在End-to-end Optimized Image Compression中使用非参数分段线性密度模型(Non-parametric piecewise linear density model)来表征整个分离先验的因素。然而该方法存在的问题是参数范围必须为有限集合且能提前预测。本论文给出了一种新的分布拟合方式。
使用CDF函数$c:\mathbb{R}\rightarrow [0,1]$,定义密度函数$p:\mathbb{R}\rightarrow\mathbb{R}^+$,遵循以下约束:
可以假定累计分布可以由多个函数构成,那么使用链式法则可以得到:
这里的$f_k$可以视为向量函数:
此处$f_K’$为$f_K$的微分,为雅可比矩阵,执行矩阵乘法。
为了确保$p(x)$能表示密度,需要保证$f_K$能映射到$[0,1]$,同时确保$p(x)\geq 0$。则进一步需要保证雅可比矩阵的元素非负。因而函数的选择可以如下所示:
这里$g_k$代表的操作为
上面的微分为
为了让微分非负,需要对$\mathbf{H}^{(k)}$的元素进行非负约束,$\mathbf{a}^{(k)}$的元素下界必须限制为-1,可以进行以下的参数重整化:
论文中的实验设定的参数为$K=4,r_1=r_2=r_3=3$,实验表明该方法能有效地拟合任意的密度分布。
Joint Autoregressive and Hierarchical Priors for Learned Image Compression
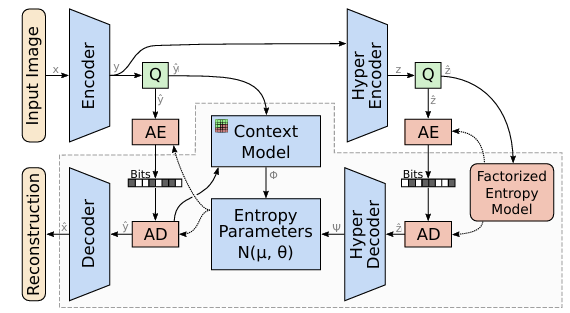
在balle2018的基础上将scale hyperprior替换为了mean-scale hyperprior,同时引入了context model。





